Algorithms - Fourier Transform
date
Dec 9, 2024
type
Post
AI summary
slug
algorithm-fourier-transform
status
Published
tags
Algorithm
summary
Discusses Fourier Transform’s in signal processing, physics, and engineering, where it converts time-domain functions into frequency-domain representations. Explains the Inverse Fourier Transform and Discrete Fourier Transform (DFT) for discrete signals. It also covers the Fast Fourier Transform (FFT), an efficient algorithm for polynomial multiplication, detailing the key steps involved in its execution and its overall time complexity of O(n log n + n). Explains how Numpy handles FFT operations with functions like
numpy.fft.fft for forward and numpy.fft.ifft for inverse transformations.Fourier Transform
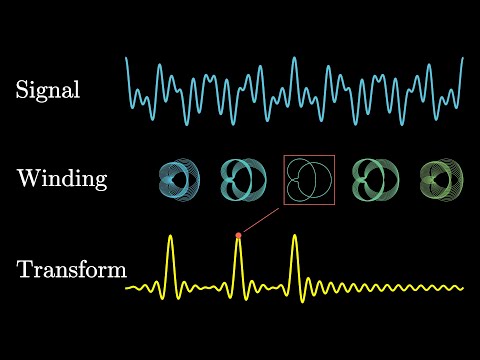
The Fourier Transform is a mathematical operation that converts a function of time (or space) into a function of frequency. It is a fundamental tool in signal processing, physics, and engineering, used to analyze the frequency components of signals or systems.
Definition
The Fourier Transform of a continuous-time signal f(t)f(t) is given by:
- : The frequency-domain representation of
- : Angular frequency (in radians per second).
- : Imaginary unit ().
The Inverse Fourier Transform recovers from :
Key Intuition
- Time to Frequency: The Fourier Transform breaks down a signal into its sine and cosine components (frequencies).
- Frequency Spectrum: represents how much of each frequency is present in .
Discrete Fourier Transform (DFT)
For discrete signals, the Fourier Transform is approximated as:
- : Frequency-domain representation ((DFT coefficients)).
- : Time-domain samples.
- : Index representing discrete frequency bins.
- : Total number of samples.
- : Index representing discrete time samples.
Frequency and Time Correspondence:
- : Corresponds to the discrete frequency index. The actual frequency is scaled by relative to the sampling frequency , i.e., .
- : Corresponds to discrete time samples.

Numpy API
numpy.fft.fft and ifft
numpy.fft.fft: Computes the Fast Fourier Transform (FFT) of a discrete time-domain signal, converting it into its frequency-domain representation. Input is the signal array, and output is a complex array representing amplitude and phase of frequency components.
numpy.fft.ifft: Computes the inverse FFT, converting frequency-domain data back to the time-domain signal. Input is the FFT result, and output is a reconstructed signal array.
- Frequency Selection: The frequencies corresponding to the FFT output are determined using the sampling frequency fsf_s and the number of samples NN. Frequencies are spaced by Δf=fsN\Delta f = \frac{f_s}{N}, ranging from 00 to fs/2f_s/2 for positive frequencies, and −fs/2f_s/2 to 00 for negative frequencies. Use
numpy.fft.fftfreqto calculate these frequencies.
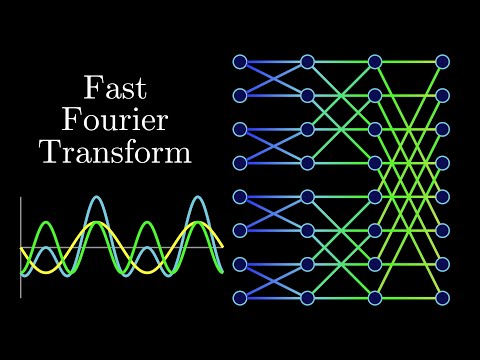
FFT for Polynomial Multiplication
FFT-based polynomial multiplication uses the Fast Fourier Transform (FFT) to efficiently compute the product of two polynomials. The Divide-and-Conquer approach splits the problem into smaller subproblems, leveraging recursion for efficient computation.
Key Steps
- Problem Setup
- Given two polynomials:
- The product:
will have a degree of
- Convert Polynomials to Point-Value Form
- Represent each polynomial as a vector of coefficients.
- Pad coefficients with zeros to the nearest power of 2 greater than .
- Recursive FFT
- Compute the FFT of the coefficient vectors for and recursively:
- Split coefficients into even and odd indexed terms.
- Recursively compute FFT for each half.
- Combine results using the symmetry of the n-th roots of unity:
where
- Pointwise Multiplication
- Multiply the FFT outputs of and pointwise:
- Inverse FFT
- Apply the Inverse FFT (IFFT) on the result to return to coefficient form.
- Result
- Extract the first coefficients of , which represent the product of and .
Time Complexity
- FFT Computation:
- Pointwise Multiplication:
- Inverse FFT:
Overall complexity: using the master theorem.